Engineering my reading list

My "Want to Read" list on Goodreads currently tallies 1'513 books. With my current pace of reading 34 books per year, it'll take me 45 years to go through them all. That's ignoring the fact that I keep adding to the list.

Alas, I simply won't be able to go through all the books that I would like to. So I have to be selective about what I read and pick only the most impactful books.

Thankfully, I've got a very specific process for doing just that!

The criteria

Given a list of books — whether filtered by topic or the whole shebang — I have to rank them, to see which ones I should prioritize. The act of ranking is basically about sorting, which in turn is all about comparing. Given two books, which one is potentially better?

To answer this, I use four different criteria to try and quantify a book's "score":

Ratings. What's the book's average rating and how many people have rated it?

Recommendations. Has anyone recommended the book to me?

References. Has any of my previously read books referenced the book?

Pages. How long would it take for me to read the book?

In summary, I want a highly-considered book, with many ratings, recommendations, and references, and a big return on invested time. Simple but the devil's in the details.

Let's have a look at each criterion, in turn, to try and define them better.

Criterion one: Ratings

Goodreads and similar cataloging services usually offer two numbers for their score: the average rating and the number of votes. These two complement each other well and give a better idea of the item's quality than just looking at an average rating.

For example, consider two books:

• Book One has a 5.0 rating with two votes.
• Book Two has a 4.8 rating with two thousand votes.

Which would you guess is the better one? Simple — the second one. If a book has gone through the scrutiny of thousands of people and still came out with a solid 4.8 rating, it's probably a damn good book.

Criterion two: Recommendations

I've been writing down pretty much every recommendation I've received, by adding the book to my reading list. I guess that's part of the reason why it keeps growing, huh?

Regrettably, only very recently did I start to also record who recommended the book. I wish I had done this sooner, as this added metadata opens up some interesting possibilities.

Now I'm able to count how many recommendations a given book has, which is something I can then use to rank it. If enough people have recommended a specific book, even one with a low average rating, I want to prioritize reading it.

As a nice added benefit, knowing who has recommended a book also allows me to thank them (or berate them, depending on how good of a book it was).

Criterion three: References

As I'm reading a book, I highlight mentions of other books. Similarly to recommendations, the more references a book has, the more likely it's a worthwhile read.

Criterion four: Pages

I loved The Dip and Principles enough to give them both a five-star review. Each delivered a powerful concept that still stays with me today. Yet, one of them managed this in 80 pages and the other took 593 pages.

Less isn't always more but, all other things being equal, I'd rather read the shorter book, so that I have more time to process the contents and write about its ideas.

The algorithm

Of course, I can't go through my thousands of book prospects and compare them one by one every time I pick my next read. Instead, I need a way to quantify all of my important criteria, so that I can rank the books and be able to choose from the highest priority.

Different criteria need different calculations, because of how they're encoded and how much weight I want to give them. Let's break them down, one by one.

Ratings

A book's rating is perhaps not the most important factor but definitely the most interesting one. How I decided to quantify it also lays the foundation for all the other factors.

The main problem here is this: how do you consolidate an average rating with its number of votes? How do you calculate it so that you can easily compare Book One with a 5.0 rating and two votes versus Book Two with a 4.8 rating and two thousand votes?

After browsing through and considering a bunch of different statistical solutions, I decided to use Bayesian Average, which seems to really shine for my specific use.

The way it works is by defining a prior probability distribution and then modifying that with the observed data, to obtain a posterior probability distribution. Basically, we make a guess, compare that to our data, and end up with a more accurate guess.

(Apologies to all the real statisticians out there, for this extreme simplification.)

Bayesian Average is defined as such:

\[ x = {C * R + c * r \over C + c} \]

• R is the first half of our guess — the average of all books' average ratings.
• C is the second half — how many votes we require for high confidence in r.
• c is the number of votes for the book we're quantifying.
• r is the average rating for the book we're quantifying.

One thing I do differently is use the logarithmic base 10 of the votes. I don't want to give too much weight to the extreme cases of books with hundred of thousand of votes, while maintaining significance for differences in the smaller number of votes.

Recommendations and references

The second part of my algorithm is a combination of recommendations from people I know and references from books I've read.

Each one is basically a vote with a pretty good rating (or else it wouldn't be recommended), yet I want to weigh these votes a lot higher than those of the many strangers on Goodreads.

The way Bayes Average works, increasing only the number of votes for a book will also bring up its total score. We'll use this to work recommendations and references into it.

10'000 votes is our threshold for a confident average rating, so we relate these two signals to that. I consider three separate recommendations or five references enough to give me the same kind of confidence. Then I can modify the book's votes like so:

\[ c + x * (C / 3) + y * (C / 5) \]

Where x is the number of recommendations and y the number of references.

Pages

Finally, and least significantly, is the number of pages.

The book's rating has likely already been influenced by this and some ideas do deserve a lot of words, so I don't want to put too much importance here.

But size can matter, at least with edge cases. I feel that books pushing past 500-600 pages usually take exponentially longer to work through, as it increases how long it takes to read the book, process my highlights, and create notes from it.

Keeping with the approach to modify the book's number of votes, I knock off 1% for every 100 pages.

\[ c * (1 - p / 100 / 100) \]

Where p is the number of pages.

The setup

With all these different parts defined, let's put them together into something useful.

We'll use the excellent tool Notion for the implementation.

I've got a database for all my books, with multiple views depending on what I want to do with them. For example, below is my process board, where I see which books I've finished reading but not yet processed (overlayed by the awesome Fahrenheit 451, which has been processed).

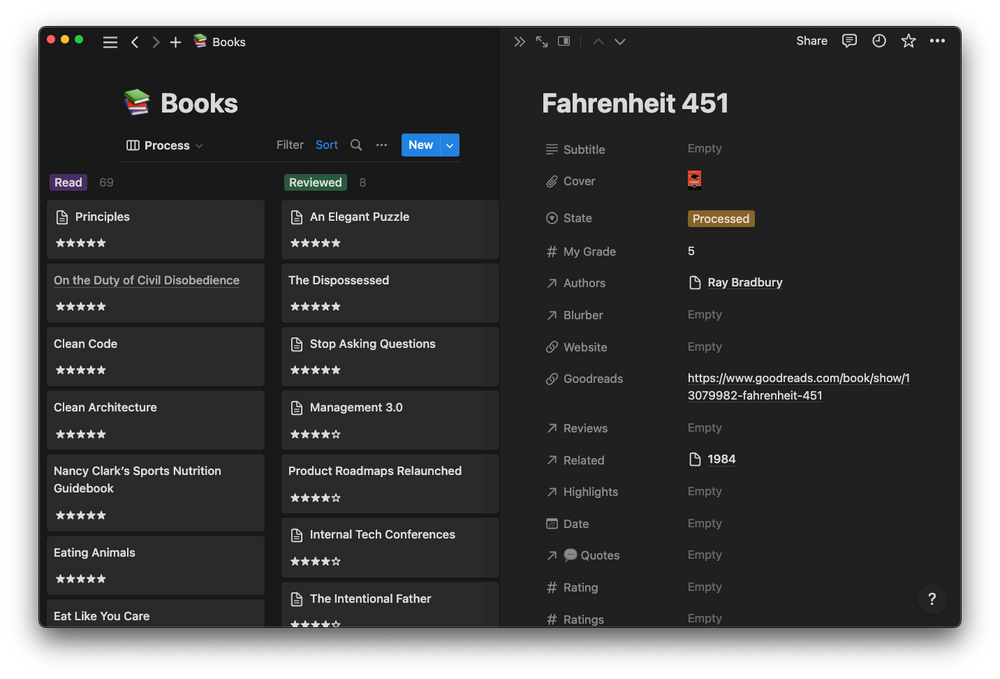
As you can see, each book has a number of properties: a subtitle, cover image, processing state, authors list, etc, etc. Some of these are what I use for my ranking.

I use references between Book pages and People pages, to keep track of recommendations, and between Book pages and other Book pages, for tracking references. These are then counted by rollup properties.

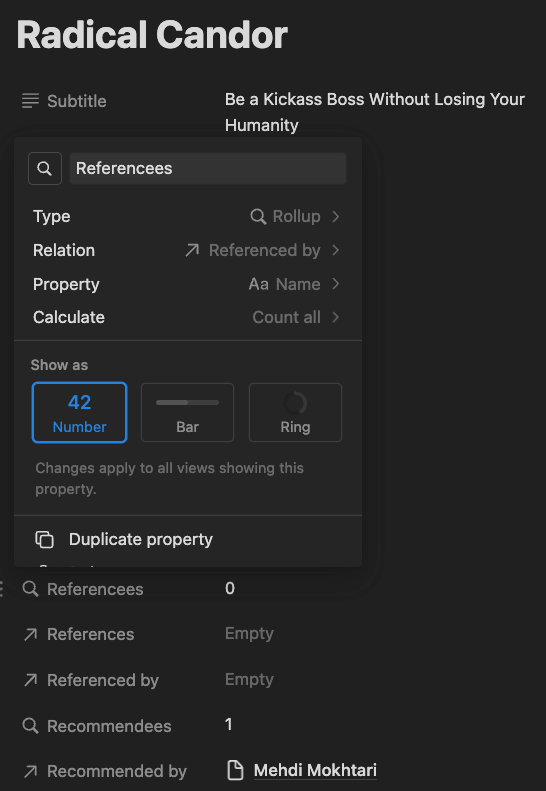
With all of the data in place, I create a formula property to calculate the final score.

(
	log10(10000) * 4
	+
	(1-prop("Pages")/100/100) * log10(
		prop("Ratings")
		+
		prop("Recommendees")*10000/3
		+
		prop("Referencees")*10000/5
	) * prop("Rating")
) / log10(10000)
+
(1-prop("Pages")/100/100) * log10(
	prop("Ratings")
	+
	prop("Recommendees")*10000/3
	+
	prop("Referencees")*10000/5
)

As a more copy/paste-friendly one-liner:

(log10(10000) * 4 + (1-prop("Pages")/100/100) * log10(prop("Ratings") + prop("Recommendees")*10000/3 + prop("Referencees")*10000/5) * prop("Rating")) / log10(10000) + (1-prop("Pages")/100/100) * log10(prop("Ratings") + prop("Recommendees")*10000/3 + prop("Referencees")*10000/5)

End result

From this, I've created a list of all my books, sorted by their final score and filtered by not-read status. This is what the top-three segment look like right now:

The top one is a very highly rated book (4.14 average ratings) with a lot of votes (180'813 to be precise) and one recommendation. That sounds about right!

The second book has a slightly lower average rating than the third (4.00 vs 4.09) but quite a lot more votes (151'660 vs 107'043) and, more importantly, one vs zero references.

I'm pretty happy with this. It gives me a lot more confidence that I'm focusing my time and energy in the right places. (Plus, it was a lot of fun to finally put this together!)

With that said, I'm no slave to this. It's just one more tool in the box, presenting me with an ordered list. I will still let my mood and curiosity get the final say in what books I pick.

There are two things missing for this to be complete, though:

1. I need to move over the tags I've added on Goodreads. Lately, for example, I've read a lot of management books and it's been a while since I immerse myself in some philosophy so that's a track I want to jump into next. If I could get a ranked list of all books within a specific tag, that'd be golden!
2. It's a bit of manual work to do all of this. Thankfully, I've already created a little Go program to integrate with Notion for some basic bookkeeping. It currently only works with my database of scientific studies (filling out data from DOIs) and I'd love to make it also synchronize my Notion database with my Goodreads lists.

As I mentioned in the intro, however, there will never be enough time to do everything one wants to. For now, this setup is good enough that I feel I can be intentional about where I spend my reading time.

I hope it helps you similarly!